读书笔记： 编码：隐匿在计算机软硬件背后的语言
第一章 至亲好友
编码这个词的意思是指一种用来在机器和人之间传递信息的方式。换句话说，编码就是交流。
问题的关键就在于数字2。两种闪烁，两种声音。事实上，两个不同的事物，只要经过适当的组合，就可以表示所有类型的信息，这的确是千真万确的。
本章小结
在本章中，我们带入小男孩的视角，想在黑夜中与街对面的朋友进行交流，本章给出了一种解决的方法，就是使用手电筒和摩尔斯电码来交流。莫尔斯电码是使用“点”和“划”来进行编码的。事实上，这种二进制的编码方式可以表示出所有的信息。
第二章 编码与组合
本章小结
作者从莫尔斯的解码引入，从而讲述了莫尔斯密码是如何计算总共有多少个组合的。由于莫尔斯码是一种二进制码，在计算的时候实际上就是2的n次幂。这一章是给没啥数学基础的小孩子讲的。
第三章 布莱叶盲文与二进制码
这64组编码中有很大一部分，根据上下文的不同将有着双重身份。
尤其值得注意的是数字标识符和取消“数字标识状态”的字母标识符。它们改变了后面编码的意义——从表示字母到表示数字，又从表示数字回到表示字母。像这样的编码通常被称作“优先码”（precedence codes）或者“换档码”（shift codes）。它们改变着作用域内编码的含义，直到作用域结束。(优先码是有开始有结束)
大写字母标识符表示紧随它的字母（而且仅仅是紧随它的字母）应该被译为大写。类似这样的编码被称为“逃逸码”（escape codes）。逃逸码让你“逃离”对编码串单调的、一成不变的解析，而转入一种新的解析方式中。(逃逸码是仅仅只有它后面的字母逃逸)
本章小结
布莱叶盲文使用了2*3的点位来表示一个字母，所以总共有64个编码。除去26个字母和10个数字之外，布莱叶盲文设计了很多的缩写、重音、以及大写标识符、数字标识符等等。其中有一定作用域范围的是“优先码”或者“换挡码”；影响力仅仅只有后面一个字母的是叫“逃逸码”
第四章 手电筒的剖析
本章小结
本章用电灯泡来引入，先介绍了一下原子、电子和电流，之后又介绍了电路的相关知识：电压、电流、电阻以及电流热效应。这也是一些初中的知识。让我们进入到下一章。
第五章 绕过拐角的通信
本章小结
本章我们又回到12岁小男孩的视角，我们现在需要和相邻房子的朋友建立起一个通讯线路来。之前我们已经学习了手电筒的内部原理。所以我们可以在两个房子之间搭建起两条手电筒电路出来。然后使用开关的开或者合来产生相应的光，使用莫尔斯电码通讯。聪明的我们可以对电路进行改进，使用公用链接的方式或者接地的方式来节省导线。
第六章 电报机与继电器
发声器中的电磁铁拉动上面的活动横杠下降，它会发出“滴”的声音。当松开电键的时候，横杠弹回到原来的位置，发出“嗒”的声音。一次快速的“滴-嗒”声代表点；一次慢速的“滴——嗒”声则代表划。
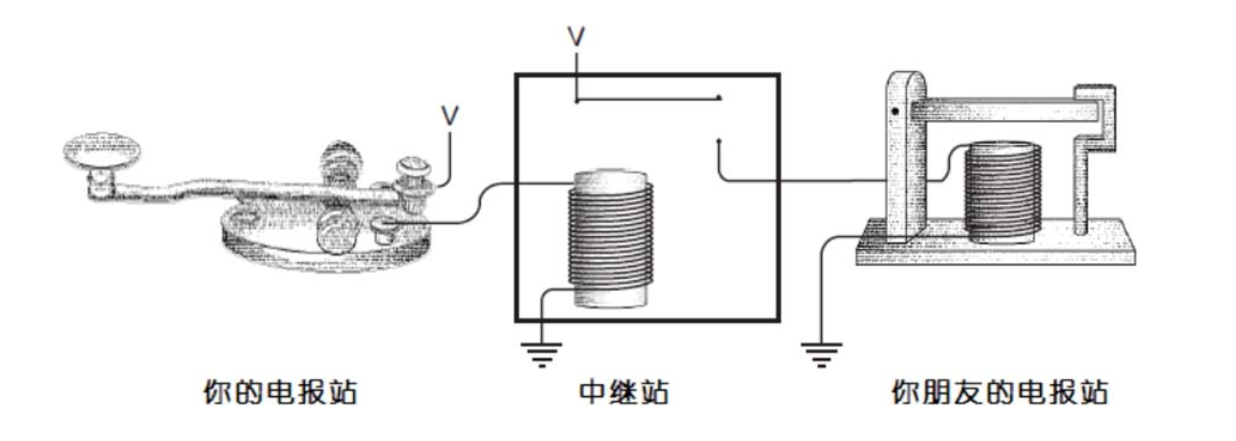
本章小结
莫尔斯不光发明了莫尔斯码，还发明了电报机和继电器。简单来说，就是使用电流的磁效应，来带动金属杆。而继电器就是在超远程线路的中间使用金属杆来控制另一个线路。从而使新的线路产生相同的编码。
第七章 我们的十个数字
本章小结
本章也很基础，介绍了一下十进制。重点介绍了基于位置计数的阿拉伯数字。为下一章的二进制打下基础。
第八章 十的代替品
本章小结
本章也很基础+1，本章是承接了上一章，介绍了八进制、四进制和二进制。
第九章 二进制数
二进制数字系统存在一点特殊性。这个特殊性就在于它是人们所能得到的最简单的数字系统。二进制数字系统中只有两个数字——0和1。
在计算机时代，比特被看做是组成信息块的基本单位。
1比特是可能存在的最小的信息量。任何小于1比特的内容都根本算不上是信息。由于1比特表示的是可能存在的最小信息量，那么复杂一些的信息就可以用多位二进制数来表达
信息是指多个可能性中的一种。
所有可以被转换成对两种或多种可能性的选择的信息，都可以用比特来表示。
利用二进制表示信息的一个额外的好处就是我们可以清楚地知道我们是否已经想到了所有的可能性。
比特在逻辑学中也很重要。逻辑学是哲学和数学的奇特融合，其主要目的就是确定某个陈述是真还是假。真和假同样可以表示为1和0
本章小结
本章是承接了上一章，介绍了二进制为什么特殊，为什么很重要。二进制是最小的进制了，但是小小的0和1却可以表示出无限的信息。
第十章 逻辑与开关
亚里士多德的逻辑学基础是三段论法
布尔发明了一种代数。在布尔代数（Boole’s algebra，现在也这样叫）中，操作数不是数字而是类（class）。简单说，一个类就是一个事物的群体，它后来也被称为集合（set）。布尔代数中使用“∪”和“∩”来代表并集和交集
本章小结
这一章主要是介绍了一下布尔代数，布尔代数的操作数是集合。它的操作有交集、并集、补集、差集等等。同时，布尔代数可以和电路的串联、并联联系起来。用灯泡的亮和暗来代表最终结果，这也是一个二进制的体现。
第十一章 门
1938年，香农在麻省理工学院完成了那篇题为《继电器和开关电路的符号分析》（A Symbolic Analysis of Relay and Switching Circuits）的著名硕士论文，在文中阐述了这个问题（10年之后，他又发表了论文“通信的数学原理”，即The Mathematical Theory ofCommunication，这是第一篇使用“bit”这个词来表示二进制数字的文章）。
继电器像开关一样，可以串联或并联在电路中执行简单的逻辑任务。这种继电器的组合叫做逻辑门（logic gates）。
这里提到的逻辑门执行“简单”逻辑任务是指逻辑门只完成最基本的功能。继电器优于开关之处就在于，继电器可以被其他继电器所控制，而不必由人工控制。这就意味着，这些简单的逻辑门组合起来可以实现更复杂的功能，例如一些简单的算术操作。
当电磁铁将金属簧片拉下来时，我们称继电器被“触发”（triggered）。当左边的开关断开的时候，铁芯的磁性消失，金属簧片回到原位。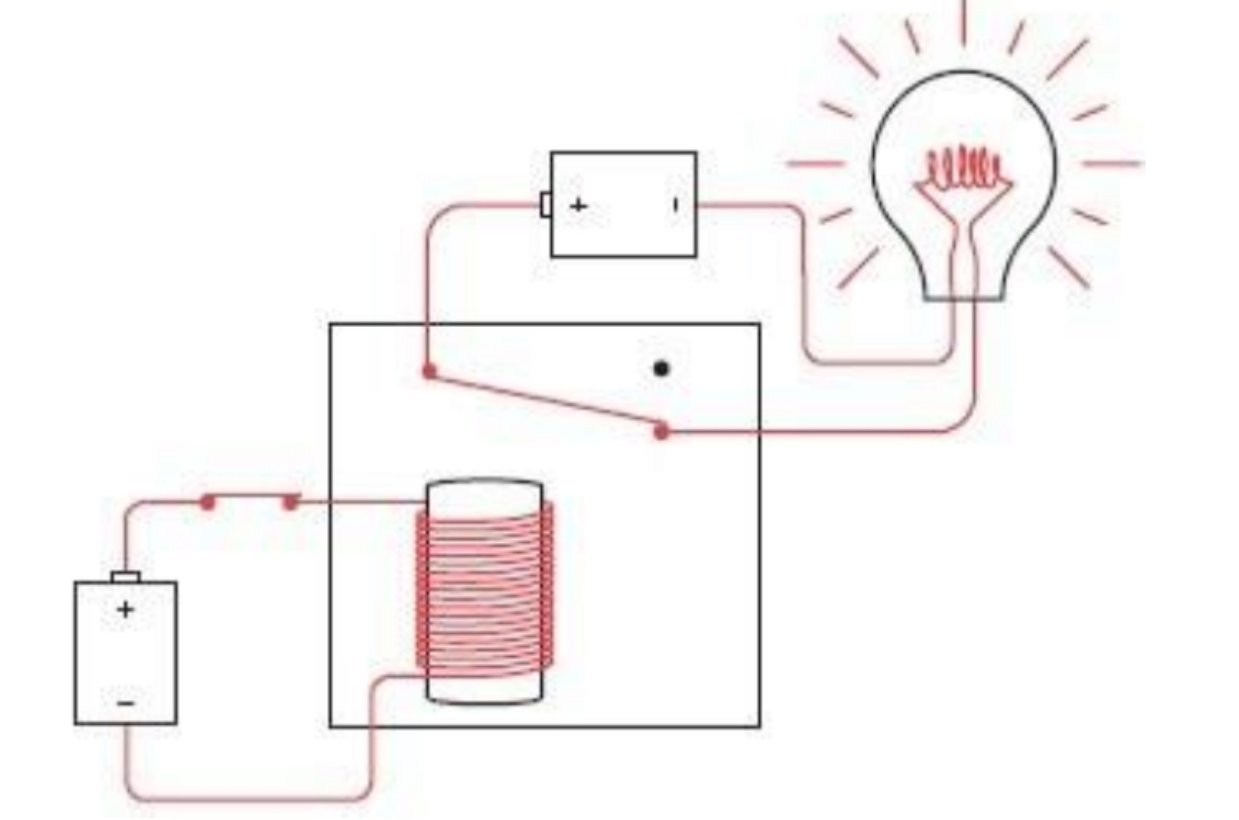
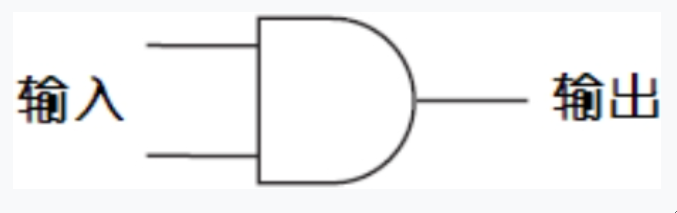
连接继电器是建立逻辑门的关键。两个开关可以串联，同样地，两个继电器也可以串联。只有两个开关都闭合的时候灯泡才会被点亮。这样的两个继电器串联被称为一个”与门“。同样也可以有三个继电器并联，这样的叫做三与门。
除了继电器串联在一起意外，继电器之间还可以并联在一起，即任意一个继电器通电，输出都会通电。我们叫它”或门”。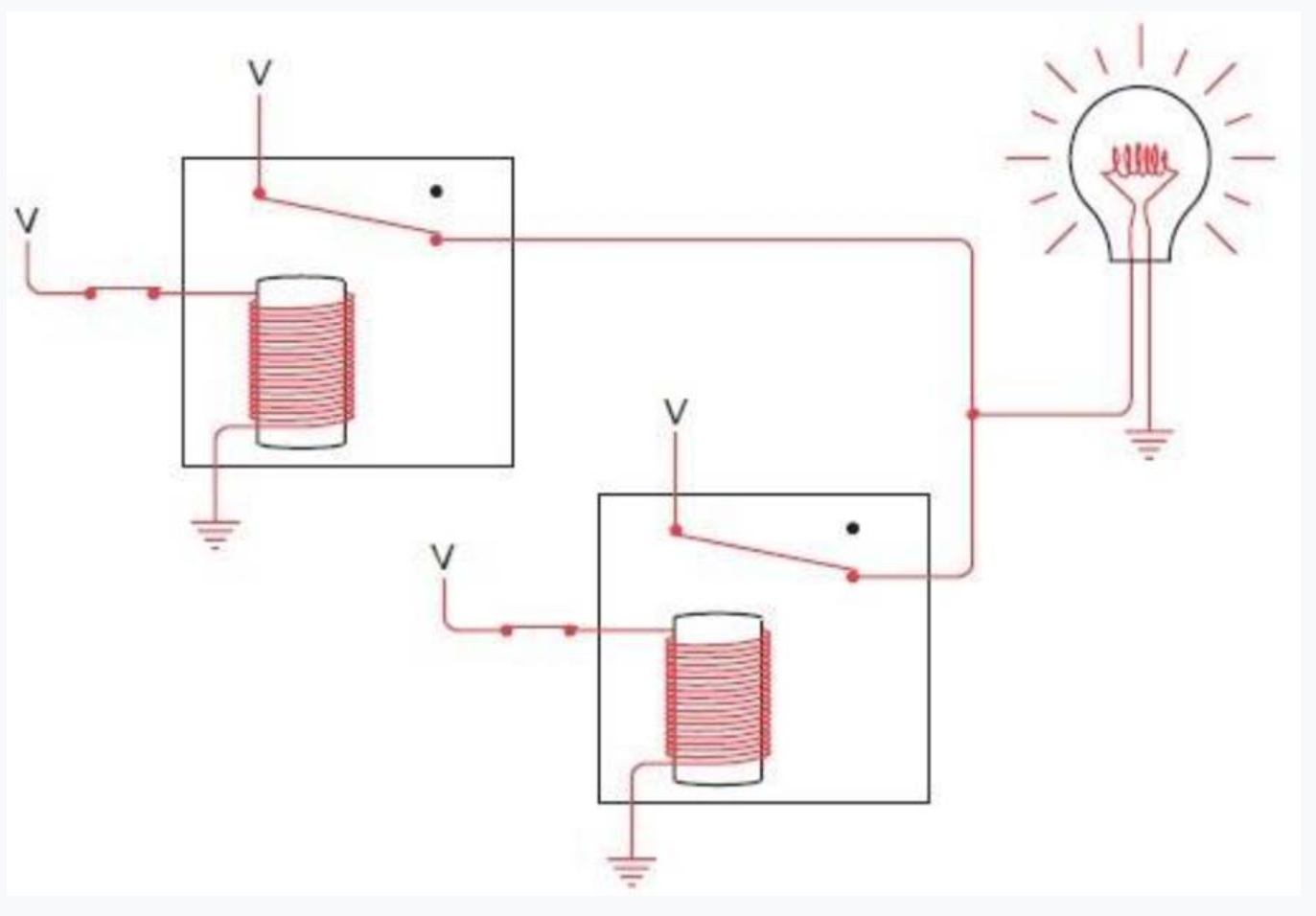
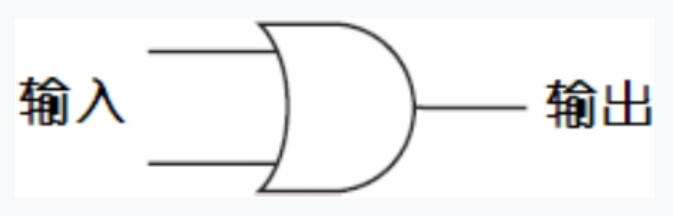
还有一种，开关闭合灯泡熄灭，开关打开灯泡亮起来。这种叫做反向器（inverter）。反向器不是逻辑门（一个逻辑门通常有两个或者多个输入），但是反向器用途很广泛，我们也可以叫他“非门”。
在连接门和反向器的时候有一些规则，影响它们的连接方式：一个门（或反向器）的输出可以作为一个或多个其他门（或反向器）的输入。但是两个或多个门（或反向器）的输出是不可以相互连接的。
恰恰与或门相反，这个门称为“或非门”，简称NOR，用以下符号表示。除去输出部分的小圆圈，这个符号与或门非常相像。小圆圈表示“反向”.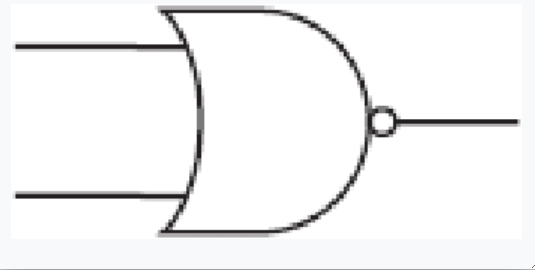
这种逻辑门被称为与非门，或简称NAND。与非门的符号和与门类似，但在输出部位多了一个小圆圈，意思是输出和与门正好相反。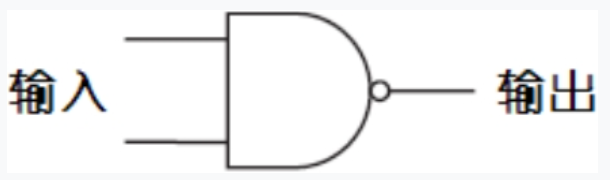
这叫做缓冲器（buffer），可用如下符号表示。除了输入端的小圆圈，这个符号与反向器是很相似的。很明显，缓冲器“没有什么作用”，它的输入与输出是相同的。但是在输入信号很微弱的时候，缓冲器就可以派上用场。另外，缓冲器还可以用于延迟一个信号。这是因为继电器需要一点时间——几分之一秒——才会被触发。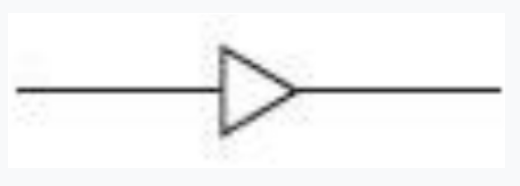
实际上，带有两个反向输入的与门和或非门是等价的。类似的，带有两个反向输入的或门和与非门也是等价的。这两组等价关系就是摩根定律在电路中的实现。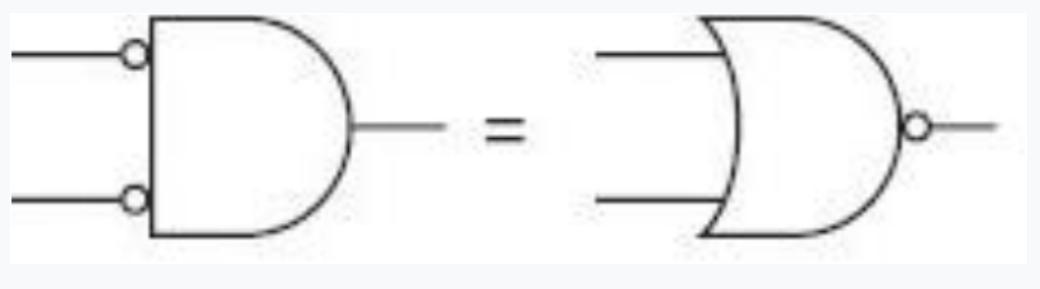
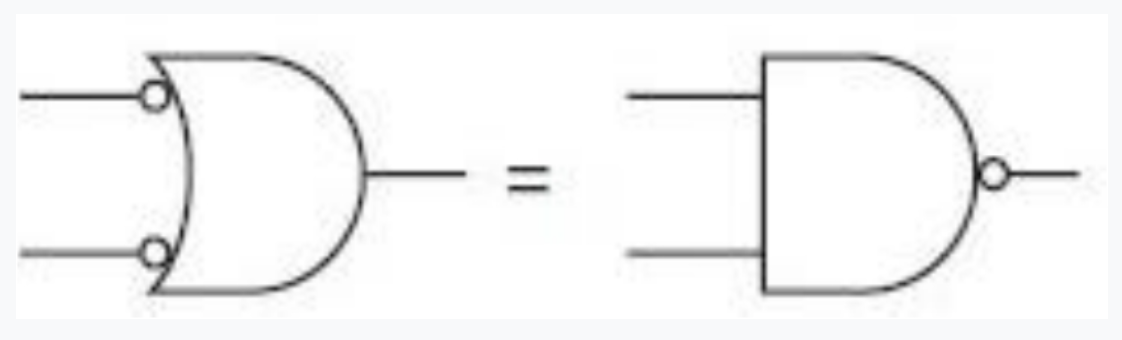
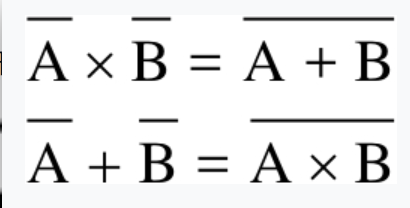
摩根定律是简化布尔表达式的一种重要手段，因此也可以用来简化电路。
本章小结
本章还是用继电器的引入，使用继电器实现了各种门。例如与门、或门、非门、与非门、或非门。最后又介绍了一下摩根定律。摩根定律也是简化布尔表达式的重要手段。现在我们就可以使用继电器来构建自己的计算机了~
第十二章 二进制加法器
加法是算术运算中最基本的运算，因此如果想搭建一台计算机。那么首先就要造出可以计算两个数的和的器件。
当你真正面对它时，就会发现，原来加法计算就是计算机要做的唯一工作。如果我们可以造出加法器，同样地，就可以利用加法来实现减法、乘法和除法
一对二进制数相加的结果中具有两个数位，其中一位叫做加法位（sum bit），另一位则叫做进位位（carry bit，例如，1加1等于0，进位为1）。
在我们的加法器中加法与进位是分别进行的。利用与门可以计算两个二进制数加法的进位。利用异或门，简写是XOR可以得到加法位。
在整个电路中仍然有两个输入和一个输出。两个输入同时作为或门和与非门的输入。或门和与非门的输出又分别作为一个与门的输入，这种叫做异或门。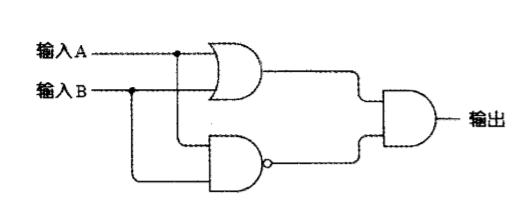
两个二进制数相加的结果是由异或门的输出给出的，而进位位是由与门的输出给出的。因此我们可以将与门和异或门连在一起来计算两个二进制数（即A和B）的和。
这个叫做半加器（Half Adder）之所以叫半加器是因为，它将两个二进制数相加，得出一个加法位和一个进位位。但是绝大多数二进制数是多于1位的。半加器没有做到的是将之前一次的加法可能产生的进位位纳入下一次运算。
首先从最左边第一个半加器的输入A和输入B开始，其输出是一个加和及相应的进位。这个和必须与前一列的进位输入相加，然后再把它们输入到第二个半加器中。第二个半加器的输出和是最后的结果。两个半加器的进位输出又被输入到一个或门中。你可能会觉得，这里还需要一个半加法器，这当然是可行的。但是如果你了解了所有的可能性之后，你会发现，两个半加法器的进位输出是不会同时为1的。或门在这里已经足够，因为或门除了在输入都为1的时候以外，其他情况下结果和异或门结果相同。
为了避免重复地画上面的那个图，我们用以下形式来替代上图中的一堆符号，它称为全加器（Full Adder）。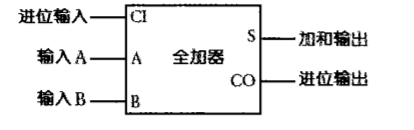
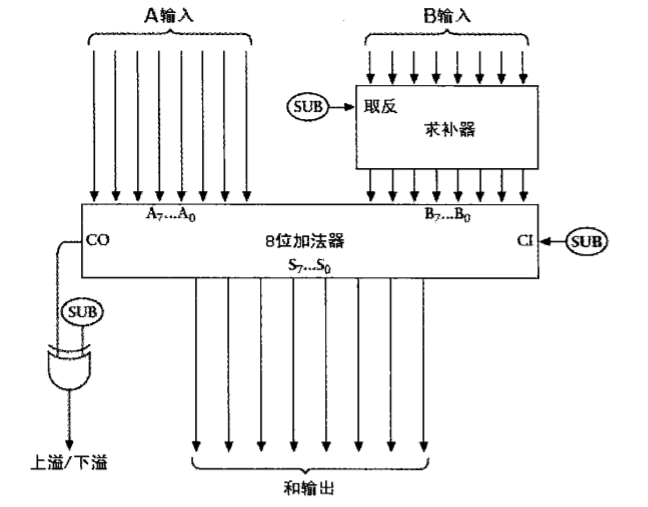
下面是画成一个盒子的完整的8位二进制加法器，输入标记为A0～A7和B0～B7，输出标记为S0～S7。A0、B0和S0是最低有效位，或者说是最右边的一位。A7、B7和S7是最高有效位，或者说是最左边的一位。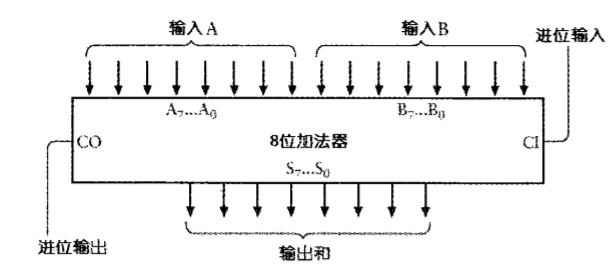
另一种8位二进制加法器可用下图表示。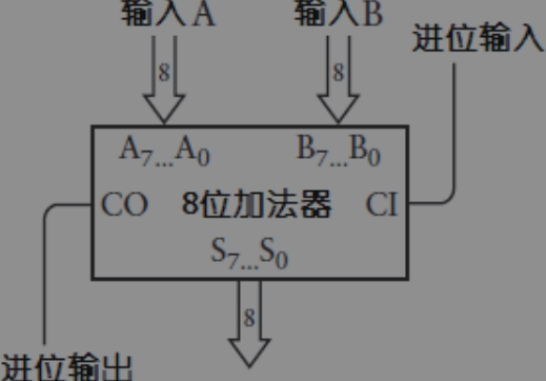
一旦你搭建起了8位二进制加法器，你就可以再搭建另外一个加法器。把它们级联起来就可以很容易地扩展出一个16位加法器。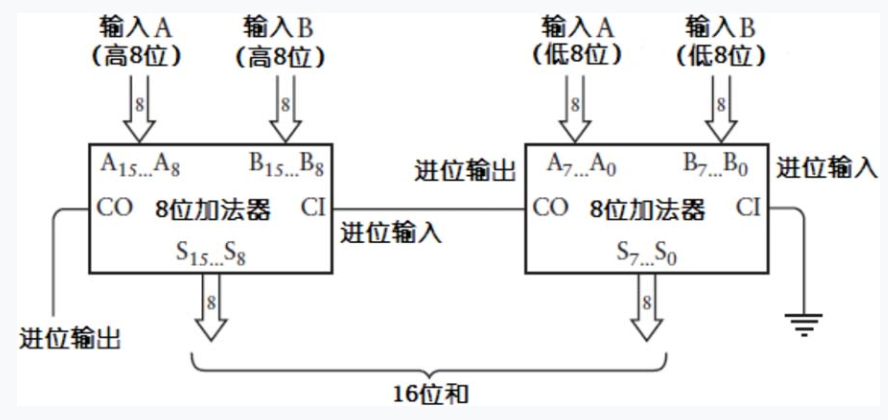
加法器的总体速度等于数字的位数乘以全加器器件的速度，这被称做行波进位（ripple carry，或脉冲进位）。更快的加法器运用了一个被称为“前置进位”的电路来提高运算的速度。
本章小结
本章主要讲述了使用逻辑门可以实现二进制的加法。两个二进制数相加的结果是由异或门的输出给出的，而进位位是由与门的输出给出的，我们就可以简单地实现一个半加器。两个半加器就可以把进位也纳入到计算中，形成一个全加器。有了全加器就可以实现8位2进制的全加器。就可以进行无限的扩展了。
而加法也是计算机计算的基础。后续的减法、乘法、除法其实都是根据加法来做的。
第十三章 如何实现减法
为了便于表达，将进行减法的两个数分别用被减数（minuend）和减数（subtrahend）表示。从被减数中减去减数，得到的结果叫做差（difference）。
为什么这种方法行得通呢？
原题目是这样的：
253- 176
在这个式子中加上一个数再减去这个数，结果是相同的。因此先加上1000，再减去1000：
253- 176 + 1000 - 1000
这个式子与下式等价：
253- 176 + 999 + 1 - 1000
然后用以下方式将数字重新组合：
253 + (999 - 176) + 1 - 1000
这就是一个求补码的过程
求补码在二进制中同样很有用，在二进制数减法中，减数是从一串1中减去的，结果称为1的补数。
我们在求对1的补数时并不需要用到减法。在求对1的补数时，只需将原来的二进制数中的1变为0，将0变为1即可。因此对1求补数有时也会称为相反数（negation）或反码（inverse）。这里你可能会想起第11章中的反向器，它的作用就是将0变为1，将1变为0。
所以二进制减法的计算过程是：第一步，用11111111（即255）减去减数；第二步，将减数对1的补数与被减数相加；第三步，将上式所得结果加1；第四步，减去100000000（即256）：
加法器中新增的主要部分就是一个用来求8位二进制数对1补数的电路。之前提到，二进制数对1求补数相当于对其每位取反，因此我们计算8位二进制数补数的时候可以简单地应用8个反向器。将8个异或门合并起来画成一个器件，称为求补器（One’sComplement），如下所示。
无符号的8位二进制数所表示的范围是0～255。有符号的8位二进制表示的范围是-128～127。无论是有符号的还是无符号的，数字本身是无法显示的。有符号现在所表示的数的范围是-128～+127。最高有效位（最左位）作为符号位（sign bit）。符号位中，1表示负数，0表示正数。
本章小结
本章介绍了二进制减法的计算和减法器的原理。二进制减法实际上就是使用加法结合律，第一步，用11111111（即255）减去减数；第二步，将减数对1的补数与被减数相加；第三步，将上式所得结果加1；第四步，减去100000000（即256）；减法器实际上就是把上述过程给实现了。然后介绍了一下有符号数和无符号数。最高有效位（最左位）作为符号位（sign bit）。符号位中，1表示负数，0表示正数。
第十四章 反馈与触发器
开关一旦闭合，金属簧片就会上下跳动——电路也会随之连通或断开——声音也就会随之发出。如果金属簧片发出了一种刺耳的声音，这套系统就成为了一个蜂鸣器。如果金属簧片前端是一把小锤子，旁边只要放上一个锣，就构成了一个电铃。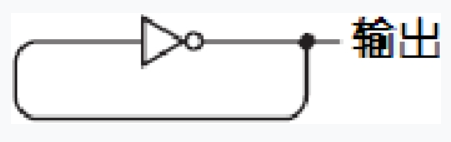
这个图可能看起来有一些逻辑矛盾，但是继电器在进行开关的开闭的时候，总会有一些时差的。所以就产生了频繁的开关闭合和打开。
我们把这种电路称为振荡器（oscillator）。在此之前我们讲过的所有的电路，其状态的改变都依靠人为的干预，通常是通过改变开关状态来实现的。但是振荡器却在不需要人干涉的情况下，可以完全自发地工作。