【读书笔记】挑战程序设计竞赛

第一章 准备篇

1.1 何谓程序设计竞赛

1. 程序时运行是有时间限制的。在大多数比赛中，运行时间限制在若干秒。一旦程序运行的时间超过了限制，程序就会被强行结束，当做不正确的解答处理。因此，在比赛中还必须考虑高效的解法。
2. 程序设计竞赛是综合了以下两个要素的复合竞赛：
   • 设计高效且正确的算法
   • 正确地实现

1.2 知名的程序设计竞赛

对我自己来说主要是侧重于Codeforces和牛客竞赛的排名

• 世界规模的大赛 – Google Code Jam (GCJ)
  已经不再举办了， https://github.com/googLe/coding-competitions-archive
• 常见的OJ：
  • PKU Online Judge(POJ) - http://poj.org/
  • Sphere Online Judge(SPOJ) - http://www.spoj.pl/
  • SGU Online Contester - http:/acm.sgu.ru/
  • UVa Online Judge - http://uva.onlinejudge.org/
  • Codeforces - http://codeforces.com/
  • Atcoder - https://atcoder.jp/
  • 牛客竞赛 - https://ac.nowcoder.com/

1.3 本书使用方法

C++在几乎所有比赛中都可用。它的运行速度快，库函数丰富，因而人气很高。本书选择C++作为所用的编程语言，并基本按照g++的规范来编写源代码。

1.4 如何提交解答

提交后的返回结果还有以下其他几种：

• Runtime Error 表示程序因为非法内存访问或未处理异常而结束。
• Memory Limit Exceeded 表示程序使用的内存超过规定的内存限制。
• Presentation Error 表示虽然程序输出的答案是对的，但是换行或空格等不符合输出格式要求。
• Output Limit Exceeded 表示程序输出了过多的内容。
• Compile Error 表示所提交的源代码没能通过编译。
• SystemError,ValidatorError 表示系统发生错误无法正常判题。

1.5 以高效的算法为目标

什么是复杂度？
在设计满足问题要求的算法时，复杂度的估算是非常重要的。我们不可能把每个想到的算法都去实现一遍看看是否足够快。应当通过估算算法的复杂度来判断所想的算法是否足够高效。
在分析复杂度时，我们通常考虑它与什么成正比，并称之为算法的阶。

第2章

2.1 最基础的“穷竭搜索”

2.1.1 递归

1. 递归：在一个函数中再次调用该函数自身的行为叫做递归。在编写一个递归函数时，函数的停止条件是必须存在的。
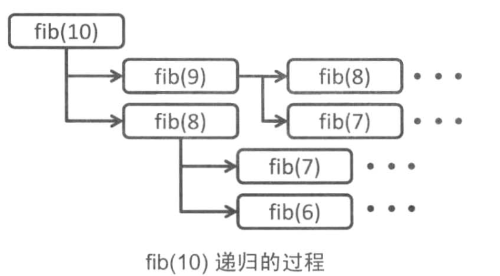
2. 在斐波那契数列中，如果fib(n)的n是一定的，无论多少次调用都会得到同样的结果。因此如果计算一次之后，用数列将结果存储起来，便可优化之后的计算。（下图中）fib(n)被调用时同样的n被计算了很多次，因此可以获得很大的优化空间。这种方法是出于记忆化搜索或者动态规划的想法。
   

2.1.2 栈

栈（Stack)是支持push和pop两种操作的数据结构。push是在栈的顶端放人一组数据的操作。反之，pop是从其顶端取出一组数据的操作。因此，最后进入栈的一组数据可以最先被取出（这种行为被叫做LIFO : Last In First Out,即后进先出）。

2.1.3 队列

队列(Queue)与栈一样支持push和pop两个操作。但与栈不同的是，pop完成的不是取出最顶端的元素，而是取出最底端的元素。也就是说最初放人的元素能够最先被取出(这种行为被叫做FIFO : First In First Out,即先进先出）。

2.1.4 深度优先搜索

深度优先搜索（DFS,Depth-First Search)是搜索的手段之一。它从某个状态开始，不断地转移状态直到无法转移，然后回退到前一步的状态，继续转移到其他状态，如此不断重复，直至找到最终的解。深度优先搜索从最开始的状态出发，遍历所有可以到达的状态。由此可以对所有的状态进行操作,或者列举出所有的状态。

2.1.5 宽度优先搜索

宽度优先搜索（BFS,Breadth-First Search)也是搜索的手段之一。它与深度优先搜索类似，从某个状态出发探索所有可以到达的状态。与深度优先搜索的不同之处在于搜索的顺序，宽度优先搜索总是先搜索距离初始状态近的状态。也就是说，它是按照开始状态 –> 只需1次转移就可以到达的所有状态 –> 只需2次转移就可以到达的所有状态–>⋯⋯这样的顺序进行搜索。对于同一个状态，宽度优先搜索只经过一次，因此复杂度为O(状态数x转移的方式)。

宽度优先搜索会把状态逐个加入队列，因此通常需要与状态数成正比的内存空间。反之，深度优先搜索是与最大的递归深度成正比的。

也有采用与宽度优先搜索类似的状态转移顺序，并且注重节约内存占用的迭代加深深度优先搜索（丨DDFS,IterativeDeepeningDepth-FirstSearch)。IDDFS是一种在最开始将深度优先搜索的递归次数限制在1次，在找到解之前不断增加递归深度的方法。

2.1.6 特殊状态的枚举

C++的标准库中提供了``next_permutation这一函数，可以把n个元素共n!`种不同的排列生成出来。又或者，通过使用位运算，可以枚举从n个元素中取出个的共C^k_n种状态或是某个集合中的全部子集等。

2.1.7 剪枝

穷竭搜索会把所有可能的解都检查一遍，当解空间非常大时，复杂度也会相应变大。比如n个元素进行排列时状态数总共有n!个，复杂度也就成了O(n!)。

深度优先搜索时，有时早已很明确地知道从当前状态无论如何转移都不会存在解。这种情况下，不再继续搜索而是直接跳过，这一方法被称作剪枝。

专栏 栈内存和堆内存

全局变量被保存在堆内存区。通常不推荐使用全局变量，但是在程序设计竞赛中，由于函数通常不是那么多，并且常常会有多个函数访问同一个数组，因此利用全局变量就很方便。

通常只需定义满足最大需要的数列大小，但如果再额外定义大一些，能很好地避免粗心导致的诸如忘记保留字符串末尾的\0的空间之类的漏洞。